应用案例
应用案例

金属表面的非接触红外测温
对几乎所有的工业生产阶段而言,遵循给定的温度值都是确保其加工与产品质量的重要因素。非接触红外测温仪是常用于测温的装置。因此,它同样也适用于金属的测温。要实现对加工温度的适当监测与控制,生产者须进行合理引导,同时消费者也应具备有关测温计数的基础知识。下文将对重要参数(诸如辐射率、反射和就此引起的测量错误)进行说明。此外,还将介绍金属测温时所受到的影响,以及如何实现可靠、可重复的测温。
在测量领域,“温度”是仅次于“时间”的常用的物理参数。红外测温装置通过吸收被测物体发出的红外辐射来测定其温度——无需接触该物体。那么,非接触测温是如何实现的呢?金属表面测温存在哪些挑战呢?
红外辐射阵列
凡是温度高于绝对零度(0 K或-273.15°C)的物体,均会自表面向外发出电磁辐射,且该辐射与物体的固有温度成比例。红外辐射阵列仅包含整个电磁辐射阵列中有限的一部分,从0.78 μm左右的可见光范围起,到1000 μm左右的波长为之。0.7 μm至14 μm是实现红外测温的重要波长范围。当波长超出该范围后,红外能量过低,以至于探测器的灵敏度不足以检测到它们,如上图所示。

当该辐射贯穿大气后,借助专用镜头便能将其聚集在探测器上。随后,探测器会生成与该辐射成比例的电信号。该信号得到放大,并通过接受连续的数字信号处理而转化为与物体温度成比例的输出信号。如此一来,在显示器上便会显示出温度的测量值,或输出为信号形式。
在将测定结果传送至控制系统时,采用的是线性0/4-20 mA、0-10 V和热电偶信号的标准化输出形式。此外,目前所使用的大多数红外测温仪都提供数字接口(USB、RS232、RS485),来实现进一步的数字信号处理,以及对装置参数的访问。
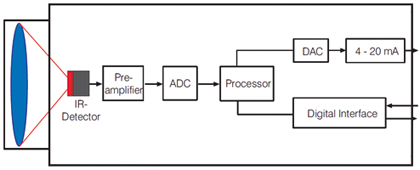
下面,我们来详细说明金属表面的红外辐射表现。首先探讨的是探测器与物体温度的信号转换。
采用红外辐射实现温度计算
作为辐射传感器的探测器识别出各红外测温仪上重要的元件。然后,在当前出现且完全可判读的电磁辐射中,生成一个信号。探测器信号U与物体温度TObject的关系如下所示:![]()
因物体发出的辐射(处于整个辐射阵列中)而产生的探测器信号与物体绝对温度的四次方成正比。也就是说:若被测物体的温度呈双倍升高,则探测器信号将呈现16倍的增大。
由于还要考虑到物体的辐射率ε、物体表面反射的周边辐射温度TAmbient、以及红外测温仪的自身辐射温度TPyro,故而公式发生改变:![]()
此外,红外测温仪并非应用于整个辐射阵列中。指数取决于波长。N代表从1μm 14 μm的波长,范围为17…2;对短波(1.0 to 2.3 μm)金属测温装置而言,该范围为15…17:![]()
物体温度值因最后一列公式的变化而增大。这些计算结果以曲线阵列的形式保存在红外测温仪的电可擦只读存储器(EEPROM)中,用于所出现的所有温度:
![]()
因此,红外测温仪接收到了足够的测温信号。从公式中可以看出,除了波长范围(辐射阵列)之外,所反射的周边辐射及辐射率也会影响到测温的准确性。这些参数的重要作用将在后文中予以说明。
黑体的重要参考作用
早在1900年,普朗克、斯蒂芬、玻尔兹曼、维恩和基尔霍夫就已详细地阐述了电磁波谱,并为说明红外能量而制定了定性与定量相干性。黑体构成了理解非接触测温技术之物理原理、以及校正红外测温仪的基础。
一方面,黑体是能够吸收所存在的一切辐射的物体。在黑体上,既没有反射(ρ = 0),也没有透射(τ = 0)。另一方面,黑体又向外发出每个波长所可能发出的最大能量(取决于其自身温度)。黑体的构造十分简单:一个带热量的中空物体,一侧末端有一个小孔。当黑体被加热至某个特定温度后,它的中空部分会形成平衡温度。
普朗克的辐射定律说明了非接触测温的基本相干性:它指出,黑体向半场中的具体光谱辐射Mλs取决于它的温度T和波长λ(c:光速;h:普朗克常数):
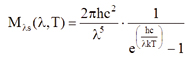
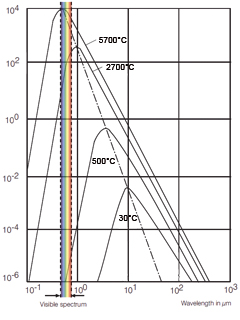
图中显示了黑体以其波长发出光谱辐射Mλs时,以对数形式呈现的温度示例。
其中可形成多种相干性,而下文仅指定了两种进行说明。通过整合所有波长下的光谱辐射密度(从0到无限大),可以得到黑体作为一个整体而发出的辐射值。这种相干性被称作斯蒂芬-玻尔兹曼定律。非接触测温的实际意义已在有关温度计算的段落中予以说明。
从上述图形轮廓中,我们可以明显得出第二种相干性,即出现最大辐射值的波长会随着温度的上升而移向短波区。这种现象成为维恩位移定律的基础,同时也能在普朗克等式的变形中得出。
因此,高辐射就是为什么能够在高温下以短波长测定金属表面温度的原因(但并非最主要的原因)。长波范围也包含了高强度。由于金属是选择性的辐射源,其辐射率、反射和因此对测量误差造成的影响都是不容小觑的。
作为选择性辐射源的金属表面
在现实中,能够满足黑体这一理想条件的物体并不多。实际上,辐射表面通常用于传感器的校正;其中,这些传感器在所需波长范围内的辐射率最大为0.99。物体温度可通过对辐射率ε(Epsilon)的辐射测量加以确定;该辐射率说明了物体实际辐射值与黑体辐射值在同一温度下的关系。因此,辐射率的取值在0到1之间:损失的辐射部分通过辐射率的显示得到补偿。
许多待测表面在多种波长下均具有恒定的辐射率,但与黑体相比,其所发出的辐射较少。它们被称作灰体。一些非金属固体可在长波光谱范围中显示出相对恒定的高辐射率,而无论其表面状况如何。
若物体(诸如金属表面)的辐射率取决于温度和波长(与其它物体相比),则此类物体被称作选择性辐射源。就“为何仅能在短波范围内进行金属测温”,存在许多重要原因。首先,在高温下处于短波范围(2.3 μm;1.6 μm;1.0 μm)内的金属表面同时呈现出最高的辐射与辐射率。其次,它们调整至金属氧化物的辐射率,这样就能最大程度的减小因改变辐射率(回火色)而造成的温差。
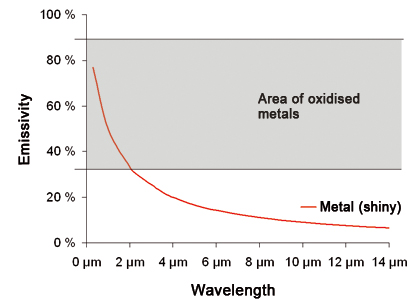
之所以决定使用短波红外测温仪,另外一个重要原因就是金属(与其它材料相比)可以具备许多未知的辐射率。短波装置能够极大地减少因辐射率的错误调整而造成的测量误差。
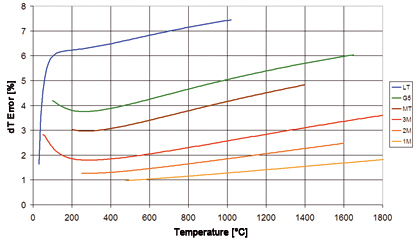
不考虑反射的可重复测量
表面辐射率越低,红外测温仪所接收到的于环境中反射的辐射率就越高。由于大多数物体(诸如金属)在红外线区域内并不存在透射,因此适用下列公式:
ε + p = 1
本式中,ε代表辐射率,ρ代表反射。从装置上判读的、转化为温度值的红外辐射不仅受到金属表面辐射率(以及补偿性的辐射部分)的影响,同时还明显受到周边环境(TAmbient)中的热物体(例如高温部件和炉子)的影响。
对参数TAmbient必须慎重考虑;待测金属表面的温度值越低,于周边环境中反射的辐射温度值就越高。实际上,反射量通常是定向的,因此易于确定。
反射量可被理解成一种尺寸,能够为可重复测量的结果提供保障。
红外测温仪的实际应用:感应式淬火与诱导过程
在感应式淬火中的热处理就是金属表面测温的一个实例。过程开始时,将一个部件放置在强交变磁场中,随后对其加热、冻结,以形成所需结构。期间,可以通过控制频率来调节渗透至材料局部的热量;在该部件上,只有局部得到了处理。要使金属材料形成所需结构,必须设置理想的温度—时间过程。因此,有必要对温度进行持续监测。
红外测温仪的重要参数为:
- 传感器探头可从电子盒上拆下;因此测温结果不会受到电磁场的干扰
- 金属表面测温专用波长(1.0 μm / 1.6 μm / 2.3 μm)
- 周围温度补偿(TAmbient),例如借助参考温度
- 在50°C至1800°C范围内,对金属进行可靠测温
- 以保持在1 ms以内的测温来实现快速温控
- 采用高光学分辨率(最小测量尺寸:0.7 mm)实现对小体积部件的测温,以及采用双激光瞄准器来标记测定区域大小




